Table of Contents
Objective:
To explore an alternative use of DNNs by implementing the style transfer algorithm.
Deliverable:
For this lab, you will need to implement the style transfer algorithm of Gatys et al.
- You must extract statistics from the content and style images
- You must formulate an optimization problem over an input image
- You must optimize the image to match both style and content
You should turn in the following:
- The final image that you generated
- Your code
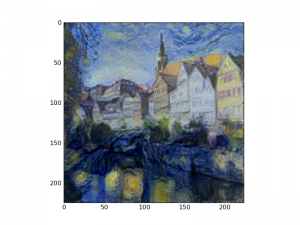
An example image that I generated is shown at the right.
Grading standards:
Your code will be graded on the following:
- 35% Correct extraction of statistics
- 35% Correct construction of cost function
- 20% Correct initialization and optimization of image variable
- 10% Awesome looking final image
Description:
For this lab, you should implement the style transfer algorithm referenced above. We are providing the following, available from a dropbox folder:
- lab10_scaffold.py - Lab 10 scaffolding code
- vgg16.py - The VGG16 model
- content.png - An example content image
- style.png - An example style image
You will also need the VGG16 pre-trained weights:
In the scaffolding code, you will find some examples of how to use the provided VGG model. (This model is a slightly modified version of code available here).
Note: In class, we discussed how to construct a computation graph that reuses the VGG network 3 times (one for content, style, and optimization images). It turns out that you don't need to do that. In fact, we merely need to evaluate the VGG network on the content and style images, and save the resulting activations.
The activations can be used to construct a cost function directly. In other words, we don't need to keep around the content/style VGG networks, because we'll never back-propagate through them.
The steps for completion of this lab are:
- Run the VGG network on the content and style images. Save the activations.
- Construct a content loss function, based on the paper
- Construct a style loss function, based on the paper
- For each layer specified in the paper (also noted in the code), you'll need to construct a Gram matrix
- That Gram matrix should match an equivalent Gram matrix computed on the style activations
- Construct an Adam optimizer, step size 0.1
- Initialize all of your variables and reload your VGG weights
- Initialize your optimization image to be the content image (or another image of your choosing)
- Optimize!
Some of these steps are already done in the scaffolding code.
Note that I ran my DNN for about 6000 steps to generate the image shown above.
Here was my loss function over time:
ITER LOSS STYLE LOSS CONTENT LOSS 0 210537.875000 210537872.00000 0.000000 100 73993.000000 67282552.000000 6710.441406 200 47634.054688 39536856.000000 8097.196777 300 36499.234375 28016930.000000 8482.302734 400 30405.132812 21805504.000000 8599.625977 500 26572.333984 17947418.000000 8624.916016 600 23952.351562 15339518.000000 8612.833008 700 22057.589844 13475838.000000 8581.751953 800 20623.390625 12093137.000000 8530.253906 900 19504.234375 11023667.000000 8480.566406 1000 18598.349609 10174618.000000 8423.731445 1100 17857.289062 9491233.000000 8366.055664 1200 17243.207031 8932358.000000 8310.849609 1300 16727.312500 8470261.000000 8257.049805 1400 16287.441406 8079912.500000 8207.528320 1500 15904.160156 7747010.500000 8157.148926 1600 15567.595703 7453235.500000 8114.359863 1700 15269.226562 7199946.500000 8069.279297 1800 15003.159180 6973264.000000 8029.895020 1900 14762.021484 6776666.500000 7985.354492 2000 14544.566406 6602410.000000 7942.156738 2100 14347.167969 6442019.000000 7905.148926 2200 14166.757812 6299105.500000 7867.651367 2300 13999.201172 6169558.500000 7829.643066 2400 13845.177734 6053753.000000 7791.424316 2500 13701.140625 5946503.500000 7754.636230 2600 13566.027344 5846906.000000 7719.121582 2700 13440.531250 5751874.500000 7688.655762 2800 13322.011719 5664197.500000 7657.814453 2900 13210.117188 5585183.000000 7624.934570 3000 13105.109375 5510268.000000 7594.841797 3100 13005.414062 5440027.500000 7565.385742 3200 12912.160156 5376126.000000 7536.033203 3300 12824.537109 5316451.500000 7508.085938 3400 12742.234375 5259337.500000 7482.895996 3500 12663.185547 5202367.500000 7460.817871 3600 12588.695312 5151772.000000 7436.922363 3700 12517.728516 5103315.000000 7414.413574 3800 12450.191406 5055678.000000 7394.513184 3900 12385.476562 5012455.000000 7373.021484 4000 12323.820312 4973657.000000 7350.163086 4100 12263.249023 4937481.000000 7325.767578 4200 12204.673828 4898750.000000 7305.923340 4300 12148.785156 4860086.000000 7288.698242 4400 12095.140625 4822883.500000 7272.257324 4500 12043.544922 4787642.500000 7255.902832 4600 11992.242188 4753499.500000 7238.742188 4700 11942.533203 4722825.500000 7219.708008 4800 11895.559570 4695372.500000 7200.187012 4900 11849.578125 4666181.000000 7183.397461 5000 11804.967773 4639222.500000 7165.745117 5100 11762.816406 4614679.500000 7148.136719 5200 11722.379883 4589744.000000 7132.635742 5300 11682.291016 4565345.000000 7116.945312 5400 11642.744141 4541704.500000 7101.039062 5500 11604.595703 4519445.000000 7085.149902 5600 11568.400391 4497892.000000 7070.507812 5700 11533.195312 4478154.000000 7055.040527 5800 11497.519531 4459191.000000 7038.328125 5900 11463.125977 4439539.000000 7023.586914 6000 11429.999023 4421518.000000 7008.480957
Hints:
You should make sure that if you initialize your image to the content image, and your loss function is strictly the content loss, that your loss is 0.0
I found that it was important to clip pixel values to be in [0,255]. To do that, every 100 iterations I extracted the image, clipped it, and then assigned it back in.
…although now that I think about it, perhaps I should have been operating on whitened images from the beginning! You should probably try that.
Bonus:
There's no official extra credit for this lab, but have some fun with it! Try different content and different styles. See if you can get nicer, higher resolution images out of it.
Also, take a look at the vgg16.py code. What happens if you swap out max pooling for average pooling?
What difference does whitening the input images make?
Show me the awesome results you can generate!