BYU CS classes

To understand the LDA model and Gibbs sampling.

For this lab, you will implement Gibbs sampling on the LDA model. You will use as data a set of about 400 General Conference talks.

Your notebook should implement two different inference algorithms on the LDA model: (1) a standard Gibbs sampler, and (2) a collapsed Gibbs sampler.

Your notebook should produce a visualization of the topics it discovers, as well as how those topics are distributed across documents. You should highlight anything interesting you may find! For example, when I ran LDA with 10 topics, I found the following topic

GS Topic 3:
                it    0.005515
          manifest    0.005188
             first    0.005022
            please    0.004463
        presidency    0.004170
          proposed    0.003997
                 m    0.003619
             favor    0.003428
           sustain    0.003165
           opposed    0.003133

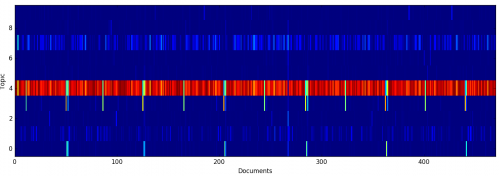
To see how documents were assigned to topics, I visualized the per-document topic mixtures as a single matrix, where color indicates probability:

Here, you can see how documents that are strongly correlated with Topic #3 appear every six months; these are the sustainings of church officers and statistical reports.

Your notebook will be graded on the following elements:

• 40% Correct implementation of Gibbs sampler
• 40% Correct implementation of collapsed Gibbs sampler
• 20% Final plots are tidy and legible

For this lab, you will code two different inference algorithms on the Latent Dirichlet Allocation (LDA) model.

You will use a dataset of general conference talks.

import numpy as np
def p( x, t=1.0 ):
    return np.exp( -10*t*((x-2)**2) ) + 0.3*np.exp( -0.5*10*t*((x+1)**2) )

This distribution has two modes that are separated by a region of low probability.

Part 1: Metropolis Hastings

For this part, you should implement the basic MH MCMC algorithm. You should use a Gaussian proposal distribution with three different variances (0.1, 1.0 and 10.0). Your sampler should start with an initial state of 0.

For each different proposal distribution, you should run your MCMC chain for 10,000 steps, and record the sequence of states. Then, you should produce a visualization of the distribution of states, and overlay a plot of the actual target distribution. They may or may not match (see, for example, the first example plot in the Description section).

Furthermore, for each proposal distribution, you should run three independent chains (you can do these sequentially or in parallel, as you like). You should display each of these three chains on a single plot with time on the x-axis and the state on the y-axis. Ideally, you will see each of the three chains mixing between two modes; you may notice other features of the behavior of the samplers as well, which you should report in your writeup!

Part 2: Hamiltonian MCMC

For this part, you will code the Hamiltonian MCMC algorithm, as discussed in class. To do this, you will need to compute the gradient of the density function with respect to the state. An easy easy way to do this is to use the autograd package:

from autograd import grad
import autograd.numpy as np
grad_p = grad( p )

The function grad_p accepts the same parameters as p, but it returns the gradient, instead of the density.

You should use the leapfrog method to integrate the dynamics.

Remember that you will need to introduce as many momentum variables as there are state (ie, position) variables.

A detailed explanation of Hamiltonian MCMC can be found here:Hamiltonian MCMC.

• You will find the equations describing the leapfrog method in Equations 5.18, 5.19 and 5.20.
• You will find a description of how to convert a given p(x) into a Hamiltonian in Section 5.3.1.
• You will find a description of the complete HMC algorithm in section 5.3.2.1

Remember that you will alternate between two steps:

1. Sampling the momentum conditioned on the position. This is just sampling from a Gaussian.
2. Proposing a new state for the position, given the momentum. This involves integrating the dynamics, and then accepting or rejecting based on integration error.

You will have to tune two parameters in order to implement HMC: the variance of the momentum variables, and the timestep used for integrating the dynamics. Experiment with both, and report your results using plots like those you prepared for Part 1.

Part 3: Observations

You have now coded two different inference algorithms, and a few variants of each. For this section, you must provide a small write-up that compares and contrasts each. Answer at least the following questions:

1. What was the acceptance rate of each algorithm? (ie, what percentage of proposals were accepted)
2. Why don't some inference algorithms explore both modes of the density?
3. Why do some algorithms stay in the same state repeatedly? Is this good or bad?
4. What were the best values for the variance of the momentum variables and the timestep you found? How did you know that they were good?

Here is some starter code to help you load and process the documents, as well as some scaffolding to help you see how your sampler might flow.

<code python> import numpy as np import re

vocab = set() docs = []

D = 472 # number of documents K = 10 # number of topics

# open each file; convert everything to lowercase and strip non-letter symbols; split into words for fileind in range( 1, D+1 ):

  foo = open( 'output%04d.txt' % fileind ).read()    
  tmp = re.sub( '[^a-z ]+', ' ', foo.lower() ).split()
  docs.append( tmp )

  for w in tmp:
      vocab.add( w )

# vocab now has unique words # give each word in the vocab a unique id ind = 0 vhash = {} vindhash = {} for i in list(vocab):

  vhash[i] = ind
  vindhash[ind] = i
  ind += 1

# size of our vocabulary V = ind

# reprocess each document and re-represent it as a list of word ids

docs_i = [] for d in docs:

  dinds = []
  for w in d:
      dinds.append( vhash[w] )
  docs_i.append( dinds )

#

qs = randomly_assign_topics( docs_i, K )

alphas = np.ones¹⁾[:,0] gammas = np.ones²⁾[:,0]

# topic distributions topics = np.zeros³⁾ # how should this be initialized?

# per-document-topic distributions pdtm = np.zeros⁴⁾ # how should this be initialized?

for iters in range(0,100):

  p = compute_data_likelihood( docs_i, qs, topics, pdtm )
  print "Iter %d, p=%.2f" % (iters,p)

  # resample per-word topic assignments qs

  # resample per-document topic mixtures pdtm

  # resample topics

<code>